排序

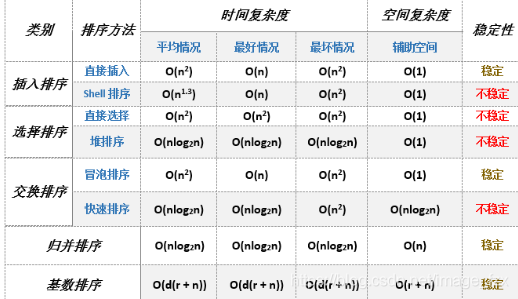
• 稳定性

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，A1=A2，且A1在A2之前，而在排序后的序列中，A1仍在A2之前，则称这种排序算法是稳定的；否则称为不稳定的。

1. 冒泡排序

将序列当中的左右元素，依次比较，保证右边的元素始终大于左边的元素； （ 第一轮结束后，序列最后一个元素一定是当前序列的最大值；） 对序列当中剩下的n-1个元素再次执行步骤1

function bubbleSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    // 因为每次比较时都已经有i个元素沉下去了，所以j<arr.length-1-i
    for (let j = 0; j < arr.length - 1 - i; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]
      }
    }
  }
  return arr
}
console.log(bubbleSort([7, 3, 4, 5, 10, 7, 8, 2]))

2. 快排

function quickSort(arr){
    if(arr.length <= 1) return arr;
    let right = [],left = [],keys = arr.shift();
    for(let value of arr){
        if(value > keys){
            right.push(value)
        }else{
            left.push(value);
        }
    }
    return quickSort(left).concat(keys,quickSort(right));
}

3. 插入排序

function insertSort(arr){
    for(let i = 1;i < arr.length;i++){
        let j = i-1;
        if(arr[i]<arr[j]){
            let temp = arr[i];
            while(j >= 0 && temp < arr[j]){
                arr[j+1] = arr[j];
                j--;
            }
            arr[j+1] = temp;
        }
    }
    return arr;
}

4. 希尔排序

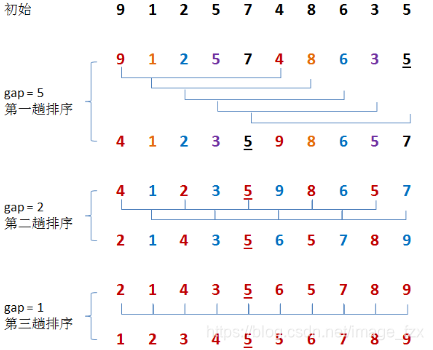
第一层循环：将gap依次折半，对序列进行分组，直到gap=1 第二、三层循环：也即直接插入排序所需要的两次循环。

function shellSort(arr) {
  let len = arr.length;
  for (let gap = Math.floor(len / 2); gap > 0; gap = Math.floor(gap / 2)) {
    for (let i = gap; i < len; i++) {
      let j = i;
      let current = arr[i];
      while(j - gap >= 0 && current < arr[j - gap]) {
        arr[j] = arr[j - gap];
        j = j - gap;
      }
      arr[j] = current;
    }
  }
}

5. 选择排序

第一层循环：依次遍历序列当中的每一个元素 第二层循环：将遍历得到的当前元素依次与余下的元素进行比较，找到最小元素的索引，与元素arr[i]交换。

function selectSort(arr){
    for(let i = 0;i < arr.length;i++){
        let min = Math.min(...arr.slice(i));
        let index = arr.indexOf(min);
        [arr[i],arr[index]] = [arr[index],arr[i]];
    }
    return arr;
}

6. 归并排序

分解----将序列每次折半拆分 合并----将划分后的序列段两两排序合并

//  分治
function MergeSort(arr,left,right){
    if(left >= right) return;
    let mid = Math.floor((right - left) >> 1) + left;
    MergeSort(arr,left,mid);
    MergeSort(arr,mid+1,right);
    Merge(arr,left,mid,right);
    return arr;
}
function Merge(arr,left,mid,right){
    let temp = [],i = 0;
    let p1 = left,p2 = mid + 1;
    while(p1 <= mid && p2 <= right){
        arr[p1] <= arr[p2] ? temp[i++] = arr[p1++] : temp[i++] = arr[p2++];
    }
    while(p1 <= mid){ temp[i++] = arr[p1++]; }
    while(p2 <= right){ temp[i++] = arr[p2++]; }
    for(let i = 0;i < temp.length;i++){
        arr[i+left] = temp[i];
    }
}

7. 堆排序

堆----完全二叉树：

每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]

每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆；arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

function adjustMaxHeap(heap,head,heapSize){
    let temp = heap[head];
    let child = head * 2 + 1;
    while(child < heapSize){
        if(child+1 < heapSize && heap[child] < heap[child+1]) child++;
        if(heap[head] < heap[child]){
            heap[head] = heap[child];
            head = child;
            child = head * 2 + 1;
        }else break;
        heap[head] = temp;
    }
}
function buildHeap(heap){
    for(let i = (heap.length-1) >> 1;i >= 0;i--){
        adjustMaxHeap(heap,i,heap.length);
    }
}
function heapSort(arr){
    buildHeap(arr);
    for(let i = arr.length-1;i > 0;i--){
        [arr[i],arr[0]] = [arr[0],arr[i]];
        adjustMaxHeap(arr,0,i);
    }
    return arr;
}